Cluster Sampling | A Simple Step-by-Step Guide with Examples
In cluster sampling, researchers divide a population into smaller groups known as clusters. They then randomly select among these clusters to form a sample.
Cluster sampling is a method of probability sampling that is often used to study large populations, particularly those that are widely geographically dispersed. Researchers usually use pre-existing units such as schools or cities as their clusters.
How to cluster sample
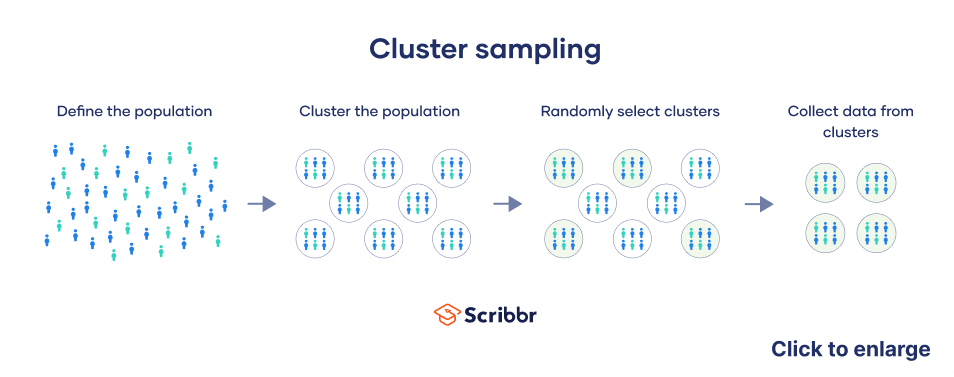
The simplest form of cluster sampling is single-stage cluster sampling. It involves 4 key steps.
It would be very difficult to obtain a list of all seventh-graders and collect data from a random sample spread across the city. However, you can easily obtain a list of all schools and collect data from a subset of these. You thus decide to use the cluster sampling method.
Step 1: Define your population
As with other forms of sampling, you must first begin by clearly defining the population you wish to study.
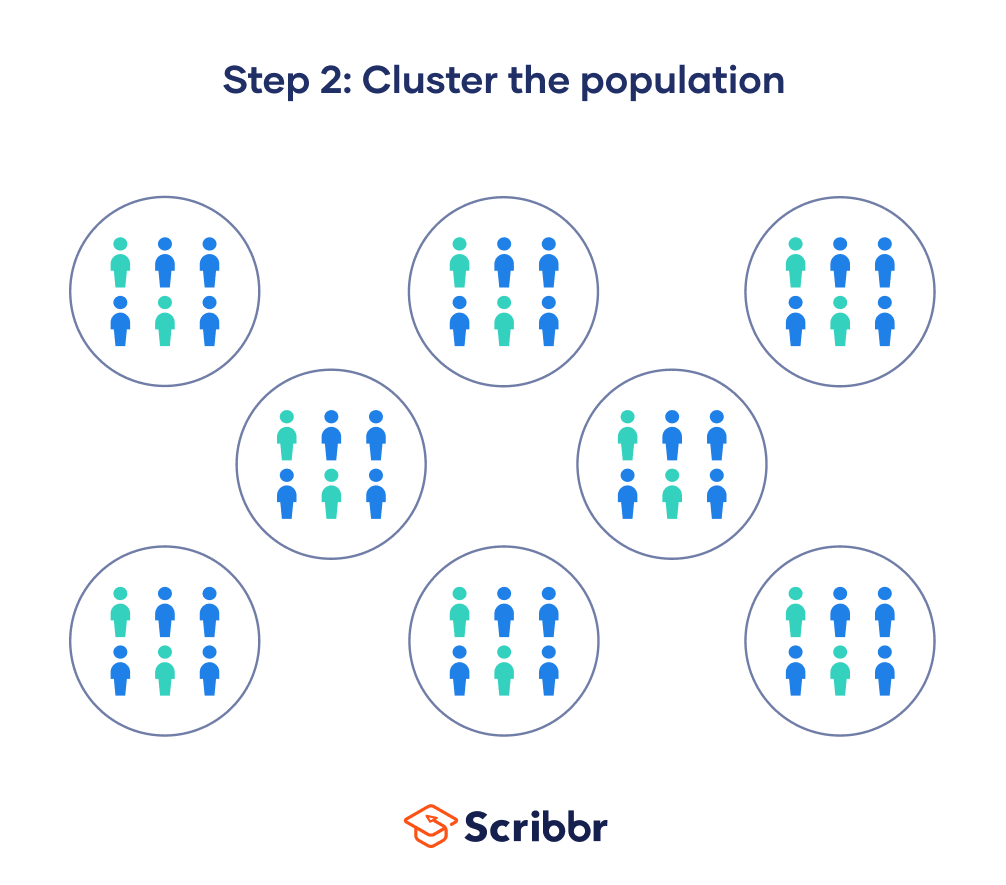
Step 2: Divide your sample into clusters
This is the most important part of the process. The quality of your clusters and how well they represent the larger population determines the validity of your results. Ideally, you would like for your clusters to meet the following criteria:
- Each cluster’s population should be as diverse as possible. You want every potential characteristic of the entire population to be represented in each cluster.
- Each cluster should have a similar distribution of characteristics as the distribution of the population as a whole.
- Taken together, the clusters should cover the entire population.
- There not be any overlap between clusters (i.e. the same people or units do not appear in more than one cluster).
Ideally, each cluster should be a mini-representation of the entire population. However, in practice, clusters often do not perfectly represent the population’s characteristics, which is why this method provides less statistical certainty than simple random sampling, and is more prone to research biases like selection bias.
Because clusters are usually naturally occurring groups, such as schools, cities, or households, they are often more homogenous than the population as a whole. You should be aware of this when performing your study, as it might affect its validity.
Step 3: Randomly select clusters to use as your sample
If each cluster is itself a mini-representation of the larger population, randomly selecting and sampling from the clusters allows you to imitate simple random sampling, which in turn supports the validity of your results.
Conversely, if the clusters are not representative, then random sampling will allow you to gather data on a diverse array of clusters, which should still provide you with an overview of the population as a whole.
You choose the number of clusters based on how large you want your sample size to be. This in turn is based on the estimated size of the entire seventh-grade population, your desired confidence interval and confidence level, and your best guess of the standard deviation (a measure of how spread apart the values in a population are) of the reading levels of the seventh-graders.
You then use a sample size calculator to estimate the required sample size.
Step 4: Collect data from the sample
You then conduct your study and collect data from every unit in the selected clusters.
Here's why students love Scribbr's proofreading services
Multistage cluster sampling
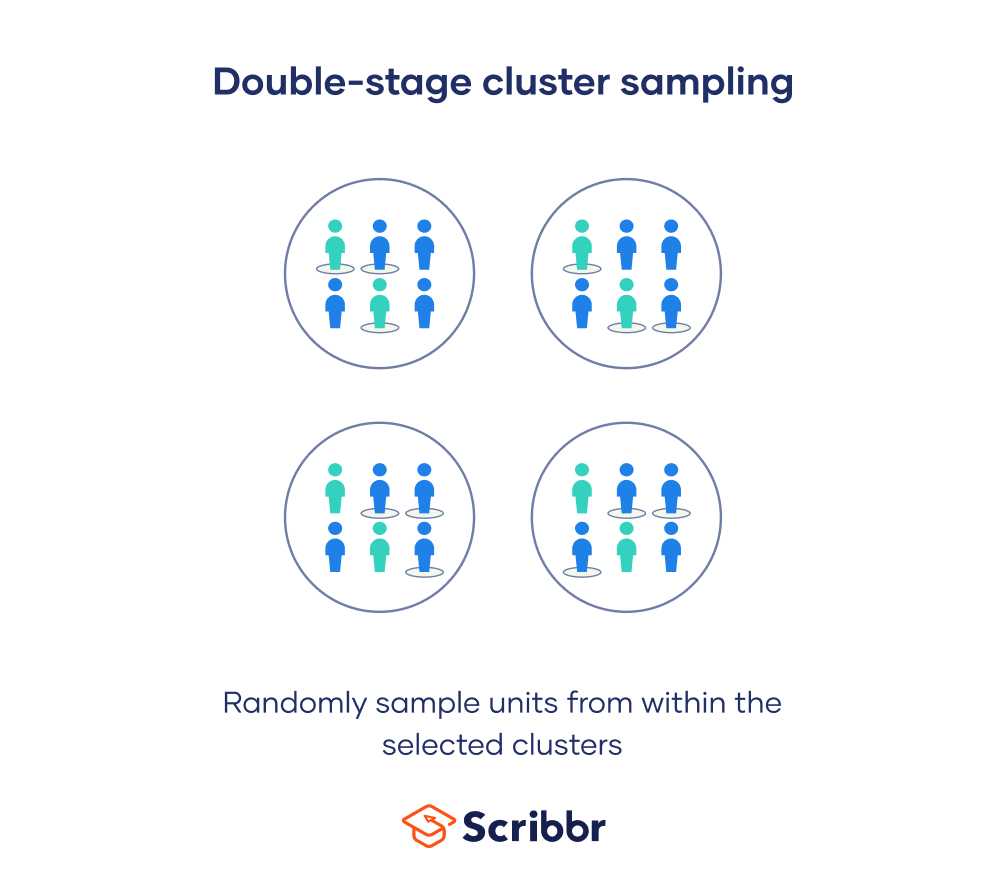
In multistage cluster sampling, rather than collect data from every single unit in the selected clusters, you randomly select individual units from within the cluster to use as your sample.
You can then collect data from each of these individual units – this is known as double-stage sampling.
You can also continue this procedure, taking progressively smaller and smaller random samples, which is usually called multistage sampling.
You should use this method when it is infeasible or too expensive to test the entire cluster.
- From each school, you randomly select a sample of seventh-grade classes.
- From within those classes, you randomly select a sample of students.
The resulting sample is much smaller and therefore easier to collect data from.
Advantages and disadvantages
Cluster sampling is commonly used for its practical advantages, but it has some disadvantages in terms of statistical validity.
Advantages
- Cluster sampling is time- and cost-efficient, especially for samples that are widely geographically spread and would be difficult to properly sample otherwise.
- Because cluster sampling uses randomization, if the population is clustered properly, your study will have high external validity because your sample will reflect the characteristics of the larger population.
Disadvantages
- Internal validity is less strong than with simple random sampling, particularly as you use more stages of clustering.
- If your clusters are not a good mini-representation of the population as a whole, then it is more difficult to rely upon your sample to provide valid results, and is very likely to be biased.
- Cluster sampling is much more complex to plan than other forms of sampling.
Other interesting articles
If you want to know more about statistics, methodology, or research bias, make sure to check out some of our other articles with explanations and examples.
Statistics
Methodology
Frequently asked questions about cluster sampling
- What is cluster sampling?
-
Cluster sampling is a probability sampling method in which you divide a population into clusters, such as districts or schools, and then randomly select some of these clusters as your sample.
The clusters should ideally each be mini-representations of the population as a whole.
- What are the types of cluster sampling?
-
There are three types of cluster sampling: single-stage, double-stage and multi-stage clustering. In all three types, you first divide the population into clusters, then randomly select clusters for use in your sample.
- In single-stage sampling, you collect data from every unit within the selected clusters.
- In double-stage sampling, you select a random sample of units from within the clusters.
- In multi-stage sampling, you repeat the procedure of randomly sampling elements from within the clusters until you have reached a manageable sample.
- What are some advantages and disadvantages of cluster sampling?
-
Cluster sampling is more time- and cost-efficient than other probability sampling methods, particularly when it comes to large samples spread across a wide geographical area.
However, it provides less statistical certainty than other methods, such as simple random sampling, because it is difficult to ensure that your clusters properly represent the population as a whole.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Thomas, L. (2023, June 22). Cluster Sampling | A Simple Step-by-Step Guide with Examples. Scribbr. Retrieved April 26, 2024, from https://www.scribbr.com/methodology/cluster-sampling/