Systematic Sampling | A Step-by-Step Guide with Examples
Systematic sampling is a probability sampling method in which researchers select members of the population at a regular interval (or k) determined in advance.
If the population order is random or random-like (e.g., alphabetical), then this method will give you a representative sample that can be used to draw conclusions about your population of interest.
When to use systematic sampling
Systematic sampling is a method that imitates many of the randomization benefits of simple random sampling, but is slightly easier to conduct.
You can use systematic sampling with a list of the entire population, like you would in simple random sampling. However, unlike with simple random sampling, you can also use this method when you’re unable to access a list of your population in advance.
Order of the population
When using systematic sampling with a population list, it’s essential to consider the order in which your population is listed to ensure that your sample is valid.
If your population is in ascending or descending order, using systematic sampling should still give you a fairly representative sample, as it will include participants from both the bottom and top ends of the population.
For example, if you are sampling from a list of individuals ordered by age, systematic sampling will result in a population drawn from the entire age spectrum. If you instead used simple random sampling, it is possible (although unlikely) that you would end up with only younger or older individuals.
You should not use systematic sampling if your population is ordered cyclically or periodically, as your resulting sample cannot be guaranteed to be representative.
If you sample every 20th individual, because each department is ordered by age, your population will consist of the oldest person in each one. This will most likely not provide a representative sample of the entire hospital population (high generalizability).
Systematic sampling without a population list
You can use systematic sampling to imitate the randomization of simple random sampling when you don’t have access to a full list of the population in advance.
Although you do not necessarily have a list of all your customers ahead of time, this method should still provide you with a representative sample of your customers since their order of exit is essentially random.
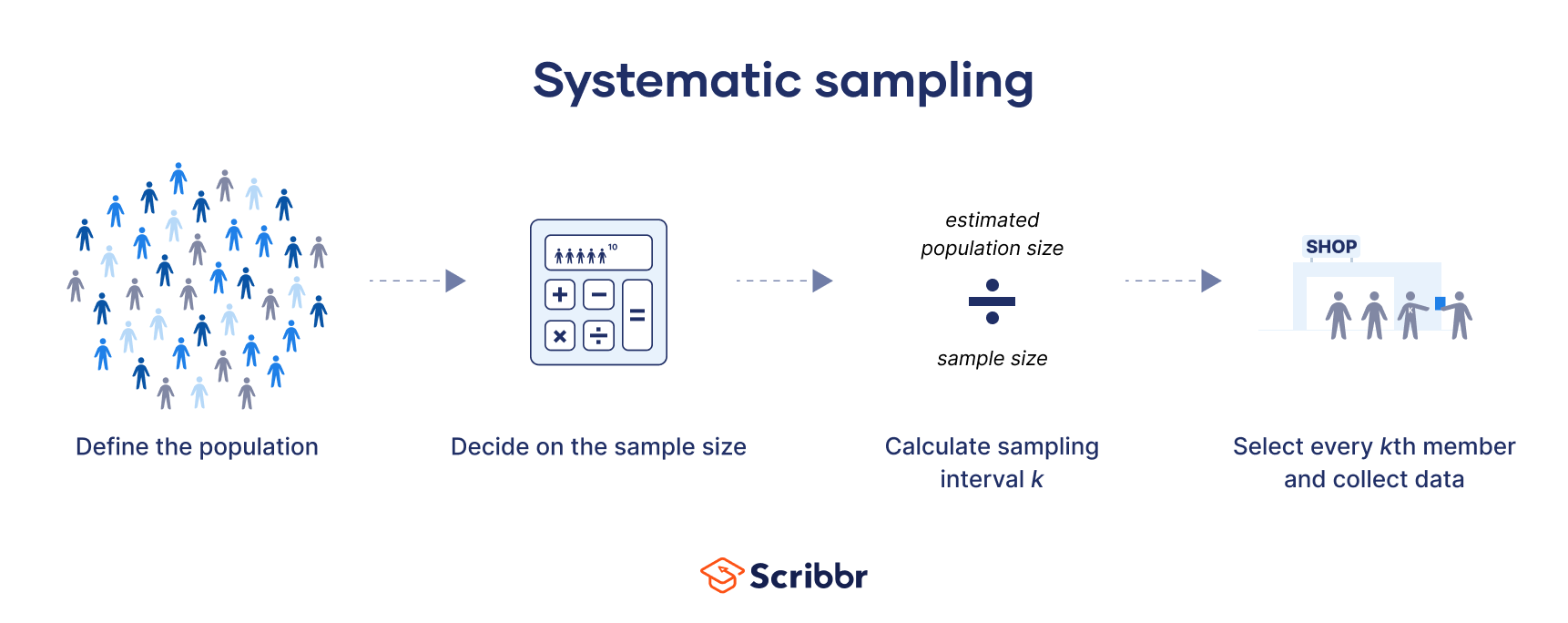
Step 1: Define your population
Like other methods of sampling, you must decide upon the population that you are studying.
In systematic sampling, you have two choices for data collection:
- You can select your sample ahead of time from a list and then approach the selected subjects to collect data, or
- You can approach every kth member of your target population to ask them to participate in your study.
Listing the population in advance
Ensure that your list contains the entire population and is not in a periodic or cyclic order. Ideally, it should be in a random or random-like (such as alphabetical) order, which will allow you to imitate the randomization benefits of simple random sampling.
However, creating such a list would be difficult, if not entirely impossible. You could choose to use receipts to create your list, but this would exclude any non-buying customers, which would most likely bias your results.
Selecting your sample on the spot
If you cannot access a list in advance, but you are able to physically observe the population, you can also use systematic sampling to select subjects at the moment of data collection.
In this case, ensure that the timing and location of your sampling procedure covers the full population to avoid bias in the results.
You must ensure that you are sampling throughout the entire week to ensure a representative sample, because different types of customers enter at different times and days: Teenagers usually shop after school and on the weekends, while working professionals might shop later in the evening and stay-at-home parents during the day.
Step 2: Decide on your sample size
Before you choose your interval, you must first decide on your sample size. It’s important to choose a representative number in order to avoid sampling bias. There are several different ways to choose a sample size, but one of the most common involves using a sample size calculator.
Once you have chosen your desired margin of error and confidence level, estimated total size of the population, and the standard deviation of the variables you are attempting to measure, this calculator will provide you with the sample size you should aim for.
Step 3: Calculate sampling interval k
When you know your target sample size, you can calculate your interval, k, by dividing your total estimated population size by your sample size. This can be a rough estimate rather than an exact calculation.
You estimate that around 7500 people visit your store each week, and based on this estimate you calculate an ideal sample size of 366. Your sampling interval k thus equals 7500/366 = 20.49, which you round to 20.
Step 4: Select the sample and collect data
If you already have a list of your population, randomly select a starting point on your list, and from there, select every kth member of the population to include in your sample.
If you don’t have a list, you choose every kth member of the population for your sample at the same time as collecting the data for your study.
As in simple random sampling, you should try to make sure every individual you have chosen for your sample actually participates in your study. If those who decide to participate do so for reasons connected with the variables that you are collecting, this could cause research bias to affect your study.
For instance, those with particularly good or bad opinions of the store may be more willing to participate than the general customer population, thus biasing the results of your survey.
Other interesting articles
If you want to know more about statistics, methodology, or research bias, make sure to check out some of our other articles with explanations and examples.
Statistics
Methodology
Frequently asked questions about systematic sampling
- What is probability sampling?
-
Probability sampling means that every member of the target population has a known chance of being included in the sample.
Probability sampling methods include simple random sampling, systematic sampling, stratified sampling, and cluster sampling.
- What is systematic sampling?
-
Systematic sampling is a probability sampling method where researchers select members of the population at a regular interval – for example, by selecting every 15th person on a list of the population. If the population is in a random order, this can imitate the benefits of simple random sampling.
- How do I perform systematic sampling?
-
There are three key steps in systematic sampling:
- Define and list your population, ensuring that it is not ordered in a cyclical or periodic order.
- Decide on your sample size and calculate your interval, k, by dividing your population by your target sample size.
- Choose every kth member of the population as your sample.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Thomas, L. (2023, December 18). Systematic Sampling | A Step-by-Step Guide with Examples. Scribbr. Retrieved April 23, 2024, from https://www.scribbr.com/methodology/systematic-sampling/