Correlation Coefficient | Types, Formulas & Examples
A correlation coefficient is a number between -1 and 1 that tells you the strength and direction of a relationship between variables.
In other words, it reflects how similar the measurements of two or more variables are across a dataset.
| Correlation coefficient value | Correlation type | Meaning |
|---|---|---|
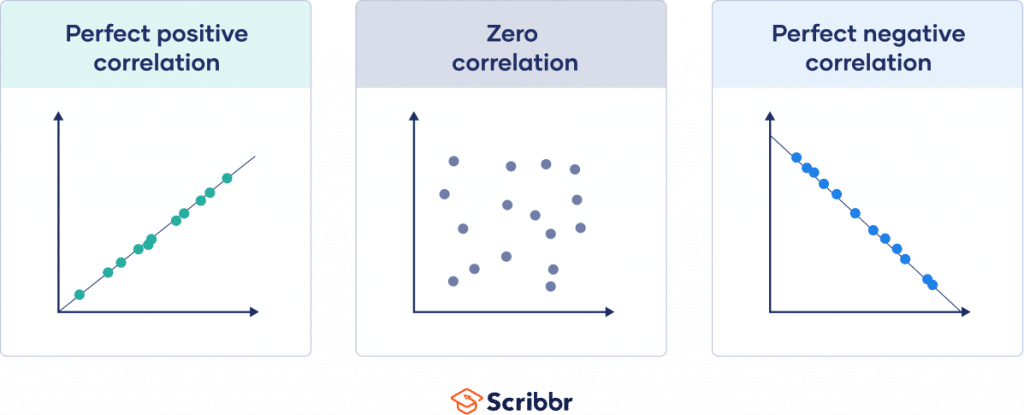
| 1 | Perfect positive correlation | When one variable changes, the other variables change in the same direction. |
| 0 | Zero correlation | There is no relationship between the variables. |
| -1 | Perfect negative correlation | When one variable changes, the other variables change in the opposite direction. |
Table of contents
- What does a correlation coefficient tell you?
- Using a correlation coefficient
- Interpreting a correlation coefficient
- Visualizing linear correlations
- Types of correlation coefficients
- Pearson’s r
- Spearman’s rho
- Other coefficients
- Other interesting articles
- Frequently asked questions about correlation coefficients
What does a correlation coefficient tell you?
Correlation coefficients summarize data and help you compare results between studies.
Summarizing data
A correlation coefficient is a descriptive statistic. That means that it summarizes sample data without letting you infer anything about the population. A correlation coefficient is a bivariate statistic when it summarizes the relationship between two variables, and it’s a multivariate statistic when you have more than two variables.
If your correlation coefficient is based on sample data, you’ll need an inferential statistic if you want to generalize your results to the population. You can use an F test or a t test to calculate a test statistic that tells you the statistical significance of your finding.
Comparing studies
A correlation coefficient is also an effect size measure, which tells you the practical significance of a result.
Correlation coefficients are unit-free, which makes it possible to directly compare coefficients between studies.
Using a correlation coefficient
In correlational research, you investigate whether changes in one variable are associated with changes in other variables.
After data collection, you can visualize your data with a scatterplot by plotting one variable on the x-axis and the other on the y-axis. It doesn’t matter which variable you place on either axis.
Visually inspect your plot for a pattern and decide whether there is a linear or non-linear pattern between variables. A linear pattern means you can fit a straight line of best fit between the data points, while a non-linear or curvilinear pattern can take all sorts of different shapes, such as a U-shape or a line with a curve.
There are many different correlation coefficients that you can calculate. After removing any outliers, select a correlation coefficient that’s appropriate based on the general shape of the scatter plot pattern. Then you can perform a correlation analysis to find the correlation coefficient for your data.
You calculate a correlation coefficient to summarize the relationship between variables without drawing any conclusions about causation.
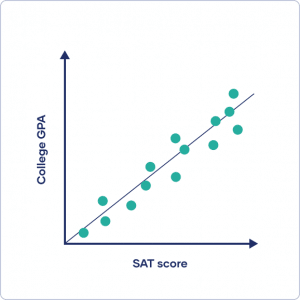
Both variables are quantitative and normally distributed with no outliers, so you calculate a Pearson’s r correlation coefficient.
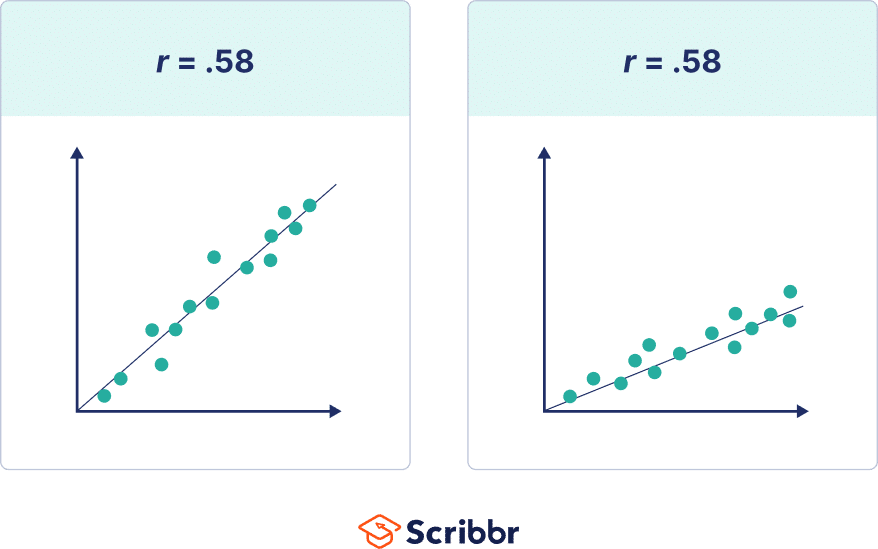
The correlation coefficient is strong at .58.
Interpreting a correlation coefficient
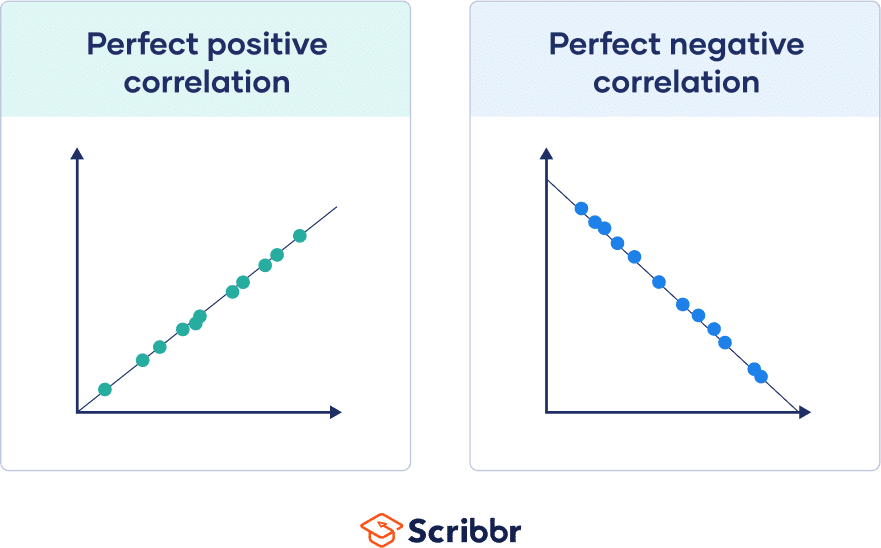
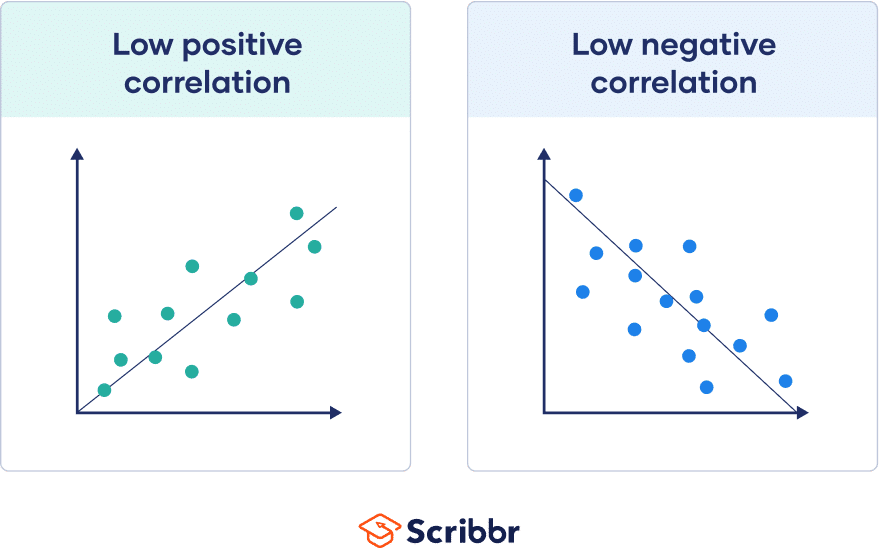
The value of the correlation coefficient always ranges between 1 and -1, and you treat it as a general indicator of the strength of the relationship between variables.
The sign of the coefficient reflects whether the variables change in the same or opposite directions: a positive value means the variables change together in the same direction, while a negative value means they change together in opposite directions.
The absolute value of a number is equal to the number without its sign. The absolute value of a correlation coefficient tells you the magnitude of the correlation: the greater the absolute value, the stronger the correlation.
There are many different guidelines for interpreting the correlation coefficient because findings can vary a lot between study fields. You can use the table below as a general guideline for interpreting correlation strength from the value of the correlation coefficient.
While this guideline is helpful in a pinch, it’s much more important to take your research context and purpose into account when forming conclusions. For example, if most studies in your field have correlation coefficients nearing .9, a correlation coefficient of .58 may be low in that context.
| Correlation coefficient | Correlation strength | Correlation type |
|---|---|---|
| -.7 to -1 | Very strong | Negative |
| -.5 to -.7 | Strong | Negative |
| -.3 to -.5 | Moderate | Negative |
| 0 to -.3 | Weak | Negative |
| 0 | None | Zero |
| 0 to .3 | Weak | Positive |
| .3 to .5 | Moderate | Positive |
| .5 to .7 | Strong | Positive |
| .7 to 1 | Very strong | Positive |
Visualizing linear correlations
The correlation coefficient tells you how closely your data fit on a line. If you have a linear relationship, you’ll draw a straight line of best fit that takes all of your data points into account on a scatter plot.
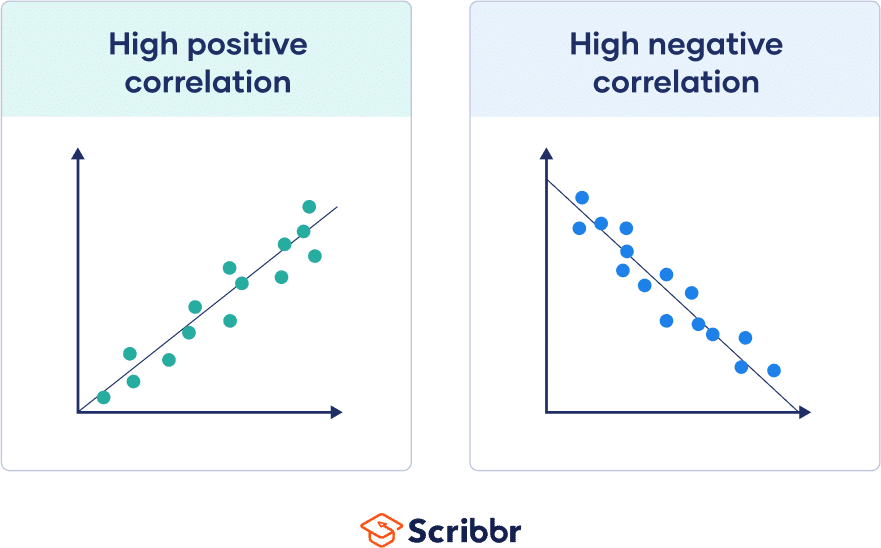
The closer your points are to this line, the higher the absolute value of the correlation coefficient and the stronger your linear correlation.
If all points are perfectly on this line, you have a perfect correlation.
If all points are close to this line, the absolute value of your correlation coefficient is high.
If these points are spread far from this line, the absolute value of your correlation coefficient is low.
Note that the steepness or slope of the line isn’t related to the correlation coefficient value. The correlation coefficient doesn’t help you predict how much one variable will change based on a given change in the other, because two datasets with the same correlation coefficient value can have lines with very different slopes.
Types of correlation coefficients
You can choose from many different correlation coefficients based on the linearity of the relationship, the level of measurement of your variables, and the distribution of your data.
For high statistical power and accuracy, it’s best to use the correlation coefficient that’s most appropriate for your data.
The most commonly used correlation coefficient is Pearson’s r because it allows for strong inferences. It’s parametric and measures linear relationships. But if your data do not meet all assumptions for this test, you’ll need to use a non-parametric test instead.
Non-parametric tests of rank correlation coefficients summarize non-linear relationships between variables. The Spearman’s rho and Kendall’s tau have the same conditions for use, but Kendall’s tau is generally preferred for smaller samples whereas Spearman’s rho is more widely used.
The table below is a selection of commonly used correlation coefficients, and we’ll cover the two most widely used coefficients in detail in this article.
| Correlation coefficient | Type of relationship | Levels of measurement | Data distribution |
|---|---|---|---|
| Pearson’s r | Linear | Two quantitative (interval or ratio) variables | Normal distribution |
| Spearman’s rho | Non-linear | Two ordinal, interval or ratio variables | Any distribution |
| Point-biserial | Linear | One dichotomous (binary) variable and one quantitative (interval or ratio) variable | Normal distribution |
| Cramér’s V (Cramér’s φ) | Non-linear | Two nominal variables | Any distribution |
| Kendall’s tau | Non-linear | Two ordinal, interval or ratio variables | Any distribution |
Pearson’s r
The Pearson’s product-moment correlation coefficient, also known as Pearson’s r, describes the linear relationship between two quantitative variables.
These are the assumptions your data must meet if you want to use Pearson’s r:
- Both variables are on an interval or ratio level of measurement
- Data from both variables follow normal distributions
- Your data have no outliers
- Your data is from a random or representative sample
- You expect a linear relationship between the two variables
The Pearson’s r is a parametric test, so it has high power. But it’s not a good measure of correlation if your variables have a nonlinear relationship, or if your data have outliers, skewed distributions, or come from categorical variables. If any of these assumptions are violated, you should consider a rank correlation measure.
The formula for the Pearson’s r is complicated, but most computer programs can quickly churn out the correlation coefficient from your data. In a simpler form, the formula divides the covariance between the variables by the product of their standard deviations.
| Formula | Explanation |
|---|---|
|
|
|
Pearson sample vs population correlation coefficient formula
When using the Pearson correlation coefficient formula, you’ll need to consider whether you’re dealing with data from a sample or the whole population.
The sample and population formulas differ in their symbols and inputs. A sample correlation coefficient is called r, while a population correlation coefficient is called rho, the Greek letter ρ.
The sample correlation coefficient uses the sample covariance between variables and their sample standard deviations.
| Sample correlation coefficient formula | Explanation |
|---|---|
|
|
|
The population correlation coefficient uses the population covariance between variables and their population standard deviations.
| Population correlation coefficient formula | Explanation |
|---|---|
|
|
|
Spearman’s rho
Spearman’s rho, or Spearman’s rank correlation coefficient, is the most common alternative to Pearson’s r. It’s a rank correlation coefficient because it uses the rankings of data from each variable (e.g., from lowest to highest) rather than the raw data itself.
You should use Spearman’s rho when your data fail to meet the assumptions of Pearson’s r. This happens when at least one of your variables is on an ordinal level of measurement or when the data from one or both variables do not follow normal distributions.
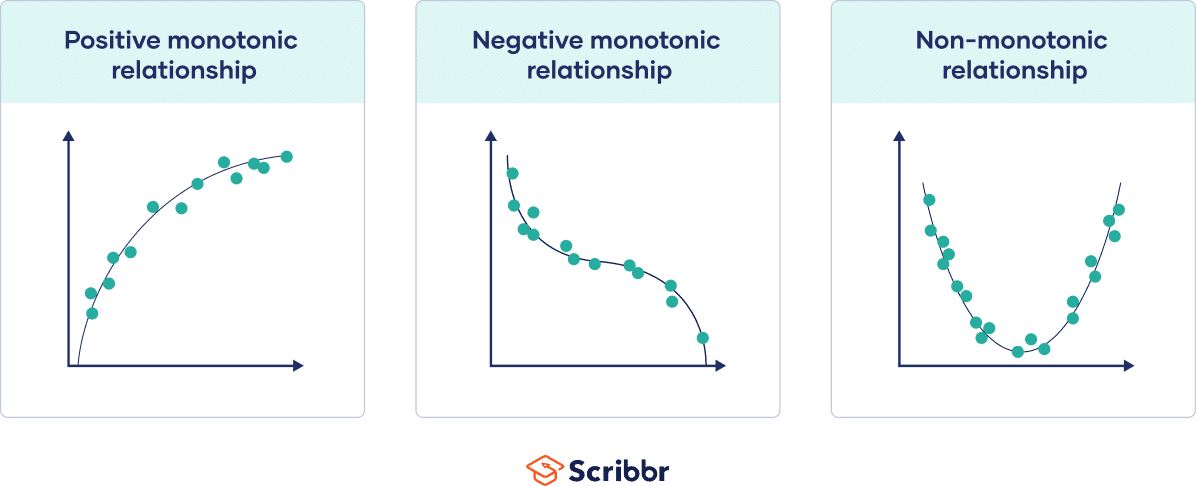
While the Pearson correlation coefficient measures the linearity of relationships, the Spearman correlation coefficient measures the monotonicity of relationships.
In a linear relationship, each variable changes in one direction at the same rate throughout the data range. In a monotonic relationship, each variable also always changes in only one direction but not necessarily at the same rate.
- Positive monotonic: when one variable increases, the other also increases.
- Negative monotonic: when one variable increases, the other decreases.
Monotonic relationships are less restrictive than linear relationships.
Spearman’s rank correlation coefficient formula
The symbols for Spearman’s rho are ρ for the population coefficient and rs for the sample coefficient. The formula calculates the Pearson’s r correlation coefficient between the rankings of the variable data.
To use this formula, you’ll first rank the data from each variable separately from low to high: every datapoint gets a rank from first, second, or third, etc.
Then, you’ll find the differences (di) between the ranks of your variables for each data pair and take that as the main input for the formula.
| Spearman’s rank correlation coefficient formula | Explanation |
|---|---|
|
|
|
If you have a correlation coefficient of 1, all of the rankings for each variable match up for every data pair. If you have a correlation coefficient of -1, the rankings for one variable are the exact opposite of the ranking of the other variable. A correlation coefficient near zero means that there’s no monotonic relationship between the variable rankings.
Other coefficients
The correlation coefficient is related to two other coefficients, and these give you more information about the relationship between variables.
Coefficient of determination
When you square the correlation coefficient, you end up with the correlation of determination (r2). This is the proportion of common variance between the variables. The coefficient of determination is always between 0 and 1, and it’s often expressed as a percentage.
| Coefficient of determination | Explanation |
|---|---|
| r2 | The correlation coefficient multiplied by itself |
The coefficient of determination is used in regression models to measure how much of the variance of one variable is explained by the variance of the other variable.
A regression analysis helps you find the equation for the line of best fit, and you can use it to predict the value of one variable given the value for the other variable.
A high r2 means that a large amount of variability in one variable is determined by its relationship to the other variable. A low r2 means that only a small portion of the variability of one variable is explained by its relationship to the other variable; relationships with other variables are more likely to account for the variance in the variable.
The correlation coefficient can often overestimate the relationship between variables, especially in small samples, so the coefficient of determination is often a better indicator of the relationship.
Coefficient of alienation
When you take away the coefficient of determination from unity (one), you’ll get the coefficient of alienation. This is the proportion of common variance not shared between the variables, the unexplained variance between the variables.
| Coefficient of alienation | Explanation |
|---|---|
| 1 – r2 | One minus the coefficient of determination |
A high coefficient of alienation indicates that the two variables share very little variance in common. A low coefficient of alienation means that a large amount of variance is accounted for by the relationship between the variables.
Other interesting articles
If you want to know more about statistics, methodology, or research bias, make sure to check out some of our other articles with explanations and examples.
Statistics
Methodology
Frequently asked questions about correlation coefficients
- What is a correlation?
-
A correlation reflects the strength and/or direction of the association between two or more variables.
- A positive correlation means that both variables change in the same direction.
- A negative correlation means that the variables change in opposite directions.
- A zero correlation means there’s no relationship between the variables.
- How many variables are in a correlation?
-
A correlation is usually tested for two variables at a time, but you can test correlations between three or more variables.
- What is a correlation coefficient?
-
A correlation coefficient is a single number that describes the strength and direction of the relationship between your variables.
Different types of correlation coefficients might be appropriate for your data based on their levels of measurement and distributions. The Pearson product-moment correlation coefficient (Pearson’s r) is commonly used to assess a linear relationship between two quantitative variables.
- What are the assumptions of the Pearson correlation coefficient?
-
These are the assumptions your data must meet if you want to use Pearson’s r:
- Both variables are on an interval or ratio level of measurement
- Data from both variables follow normal distributions
- Your data have no outliers
- Your data is from a random or representative sample
- You expect a linear relationship between the two variables
- What do the sign and value of the correlation coefficient tell you?
-
Correlation coefficients always range between -1 and 1.
The sign of the coefficient tells you the direction of the relationship: a positive value means the variables change together in the same direction, while a negative value means they change together in opposite directions.
The absolute value of a number is equal to the number without its sign. The absolute value of a correlation coefficient tells you the magnitude of the correlation: the greater the absolute value, the stronger the correlation.
- Is the correlation coefficient the same as the slope of the line?
-
No, the steepness or slope of the line isn’t related to the correlation coefficient value. The correlation coefficient only tells you how closely your data fit on a line, so two datasets with the same correlation coefficient can have very different slopes.
To find the slope of the line, you’ll need to perform a regression analysis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 22). Correlation Coefficient | Types, Formulas & Examples. Scribbr. Retrieved April 22, 2024, from https://www.scribbr.com/statistics/correlation-coefficient/