Type I & Type II Errors | Differences, Examples, Visualizations

In statistics, a Type I error is a false positive conclusion, while a Type II error is a false negative conclusion.

Making a statistical decision always involves uncertainties, so the risks of making these errors are unavoidable in hypothesis testing.

The probability of making a Type I error is the significance level, or alpha (α), while the probability of making a Type II error is beta (β). These risks can be minimized through careful planning in your study design.

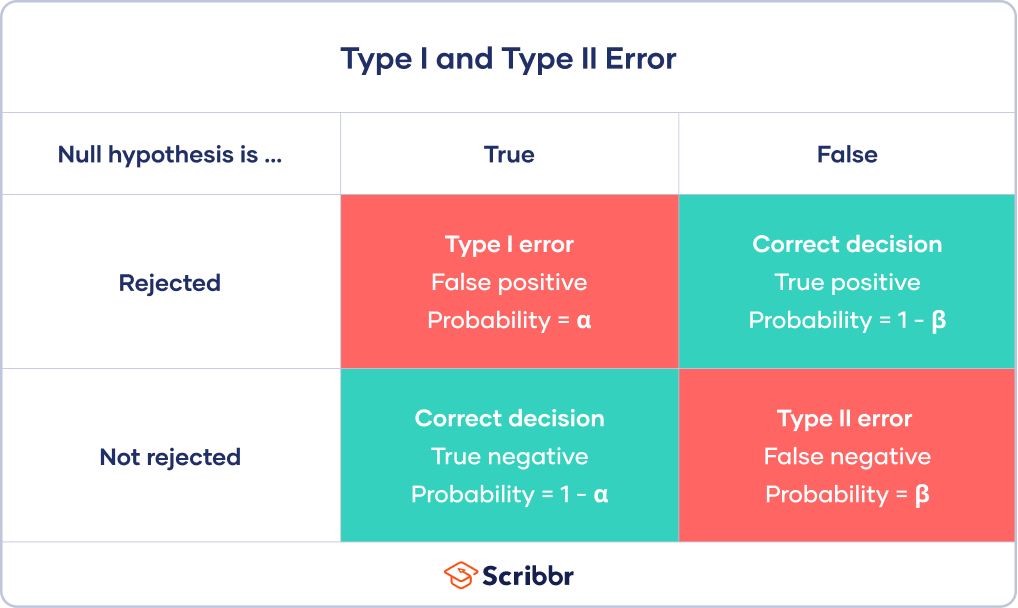
Error in statistical decision-making

Using hypothesis testing, you can make decisions about whether your data support or refute your research predictions with null and alternative hypotheses.

Hypothesis testing starts with the assumption of no difference between groups or no relationship between variables in the population—this is the null hypothesis. It’s always paired with an alternative hypothesis, which is your research prediction of an actual difference between groups or a true relationship between variables.

Then, you decide whether the null hypothesis can be rejected based on your data and the results of a statistical test. Since these decisions are based on probabilities, there is always a risk of making the wrong conclusion.

• If your results show statistical significance, that means they are very unlikely to occur if the null hypothesis is true. In this case, you would reject your null hypothesis. But sometimes, this may actually be a Type I error.
• If your findings do not show statistical significance, they have a high chance of occurring if the null hypothesis is true. Therefore, you fail to reject your null hypothesis. But sometimes, this may be a Type II error.

Type I error

A Type I error means rejecting the null hypothesis when it’s actually true. It means concluding that results are statistically significant when, in reality, they came about purely by chance or because of unrelated factors.

The risk of committing this error is the significance level (alpha or α) you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results (p value).

The significance level is usually set at 0.05 or 5%. This means that your results only have a 5% chance of occurring, or less, if the null hypothesis is actually true.

If the p value of your test is lower than the significance level, it means your results are statistically significant and consistent with the alternative hypothesis. If your p value is higher than the significance level, then your results are considered statistically non-significant.

To reduce the Type I error probability, you can simply set a lower significance level.

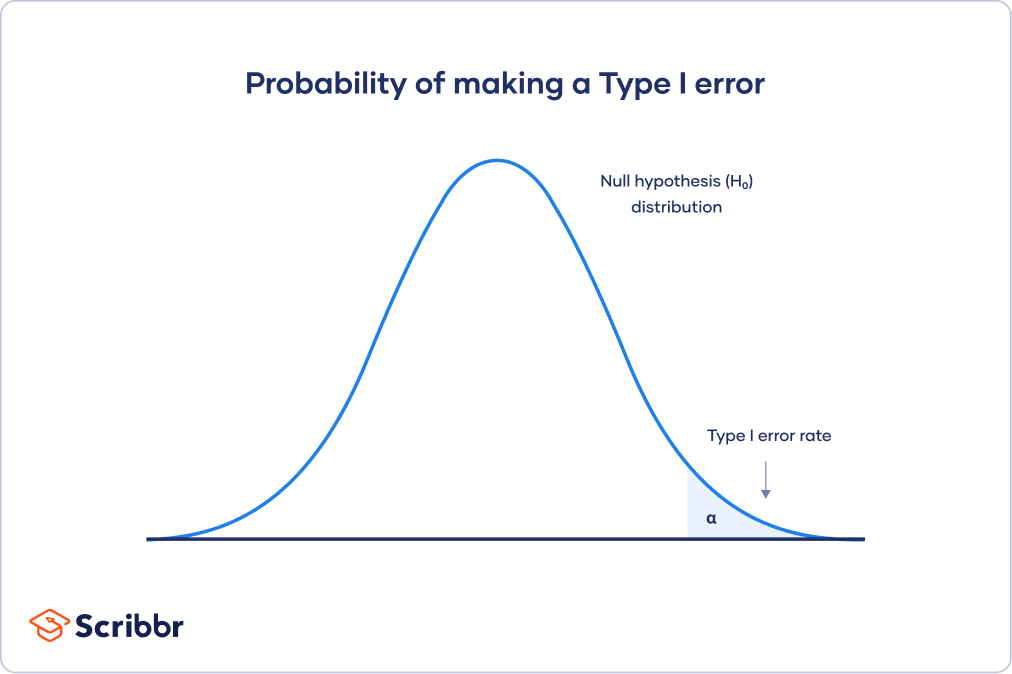
Type I error rate

The null hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the null hypothesis were true in the population.

At the tail end, the shaded area represents alpha. It’s also called a critical region in statistics.

If your results fall in the critical region of this curve, they are considered statistically significant and the null hypothesis is rejected. However, this is a false positive conclusion, because the null hypothesis is actually true in this case!

Type II error

A Type II error means not rejecting the null hypothesis when it’s actually false. This is not quite the same as “accepting” the null hypothesis, because hypothesis testing can only tell you whether to reject the null hypothesis.

Instead, a Type II error means failing to conclude there was an effect when there actually was. In reality, your study may not have had enough statistical power to detect an effect of a certain size.

Power is the extent to which a test can correctly detect a real effect when there is one. A power level of 80% or higher is usually considered acceptable.

The risk of a Type II error is inversely related to the statistical power of a study. The higher the statistical power, the lower the probability of making a Type II error.

Statistical power is determined by:

• Size of the effect: Larger effects are more easily detected.
• Measurement error: Systematic and random errors in recorded data reduce power.
• Sample size: Larger samples reduce sampling error and increase power.
• Significance level: Increasing the significance level increases power.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level.

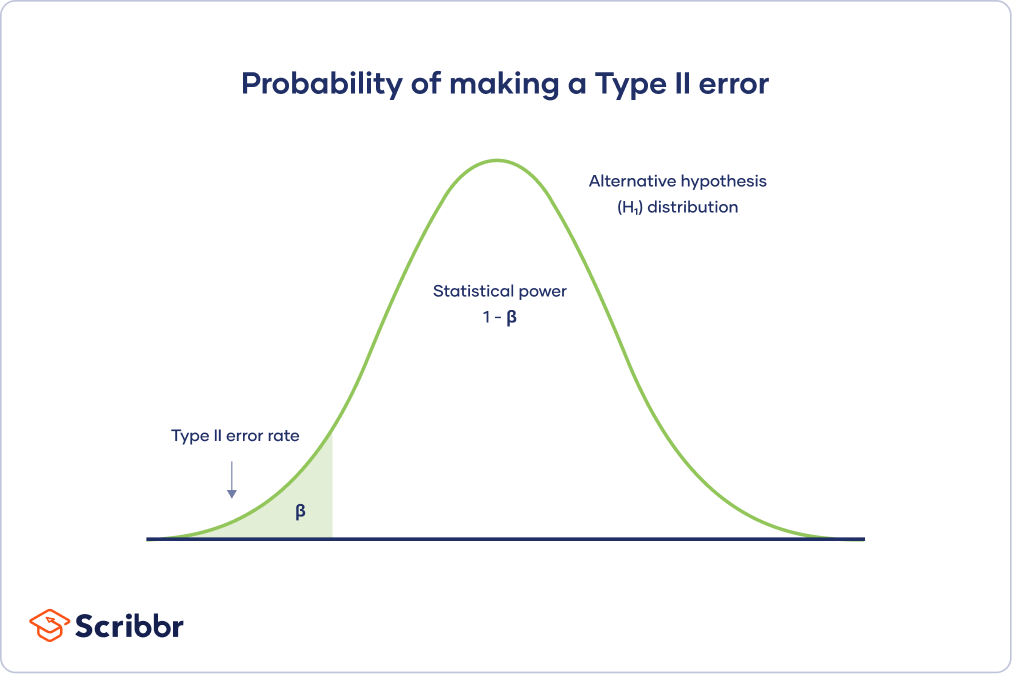
Type II error rate

The alternative hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the alternative hypothesis were true in the population.

The Type II error rate is beta (β), represented by the shaded area on the left side. The remaining area under the curve represents statistical power, which is 1 – β.

Increasing the statistical power of your test directly decreases the risk of making a Type II error.

Trade-off between Type I and Type II errors

The Type I and Type II error rates influence each other. That’s because the significance level (the Type I error rate) affects statistical power, which is inversely related to the Type II error rate.

This means there’s an important tradeoff between Type I and Type II errors:

• Setting a lower significance level decreases a Type I error risk, but increases a Type II error risk.
• Increasing the power of a test decreases a Type II error risk, but increases a Type I error risk.

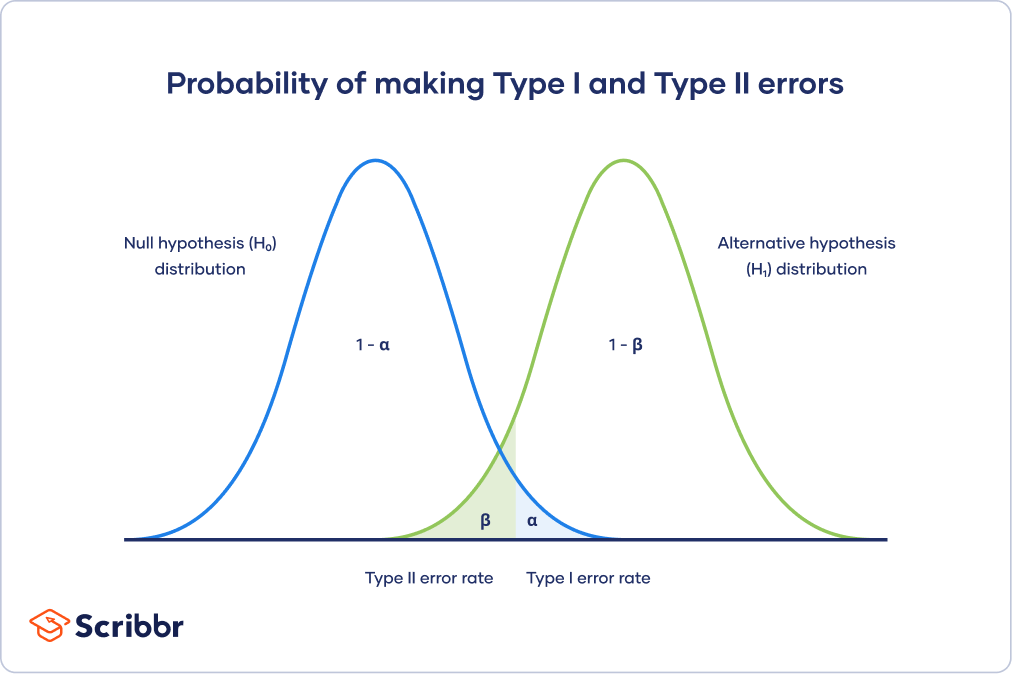
This trade-off is visualized in the graph below. It shows two curves:

• The null hypothesis distribution shows all possible results you’d obtain if the null hypothesis is true. The correct conclusion for any point on this distribution means not rejecting the null hypothesis.
• The alternative hypothesis distribution shows all possible results you’d obtain if the alternative hypothesis is true. The correct conclusion for any point on this distribution means rejecting the null hypothesis.

Type I and Type II errors occur where these two distributions overlap. The blue shaded area represents alpha, the Type I error rate, and the green shaded area represents beta, the Type II error rate.

By setting the Type I error rate, you indirectly influence the size of the Type II error rate as well.

It’s important to strike a balance between the risks of making Type I and Type II errors. Reducing the alpha always comes at the cost of increasing beta, and vice versa.

Is a Type I or Type II error worse?

For statisticians, a Type I error is usually worse. In practical terms, however, either type of error could be worse depending on your research context.

A Type I error means mistakenly going against the main statistical assumption of a null hypothesis. This may lead to new policies, practices or treatments that are inadequate or a waste of resources.

In contrast, a Type II error means failing to reject a null hypothesis. It may only result in missed opportunities to innovate, but these can also have important practical consequences.

Other interesting articles

If you want to know more about statistics, methodology, or research bias, make sure to check out some of our other articles with explanations and examples.

Frequently asked questions about Type I and II errors

What are Type I and Type II errors?

In statistics, a Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s actually false.

How do you reduce the risk of making a Type I error?

The risk of making a Type I error is the significance level (or alpha) that you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results (p value).

The significance level is usually set at 0.05 or 5%. This means that your results only have a 5% chance of occurring, or less, if the null hypothesis is actually true.

To reduce the Type I error probability, you can set a lower significance level.

How do you reduce the risk of making a Type II error?

The risk of making a Type II error is inversely related to the statistical power of a test. Power is the extent to which a test can correctly detect a real effect when there is one.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level to increase statistical power.

What is statistical significance?

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test. Significance is usually denoted by a p-value, or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis.

When the p-value falls below the chosen alpha value, then we say the result of the test is statistically significant.

What is statistical power?

In statistics, power refers to the likelihood of a hypothesis test detecting a true effect if there is one. A statistically powerful test is more likely to reject a false negative (a Type II error).

If you don’t ensure enough power in your study, you may not be able to detect a statistically significant result even when it has practical significance. Your study might not have the ability to answer your research question.